Spinning Out of Control: the physics behind impossible aerials, and the reason why they are so damn difficult
By Harapan Ong
I am not a cardist, but I understand that cardistry is an art focused on the beautiful motion of playing cards in our hands. In a skilled cardist’s hands, an ordinary deck of playing cards can take on a multitude of dazzling forms, with cards flying, flipping, and spinning around gracefully and sometimes ferociously.
In this article, I will focus on aerial moves – to be specific, the physics of aerial moves. Aerial moves, as the name suggests, are all about cards flying and moving freely in the air. From small moves like the T.G. Murphy Deck Flip, to larger scale aerials like Flicker Shot, aerial moves are some of the most eye-catching and impressive card flourishes you can do.
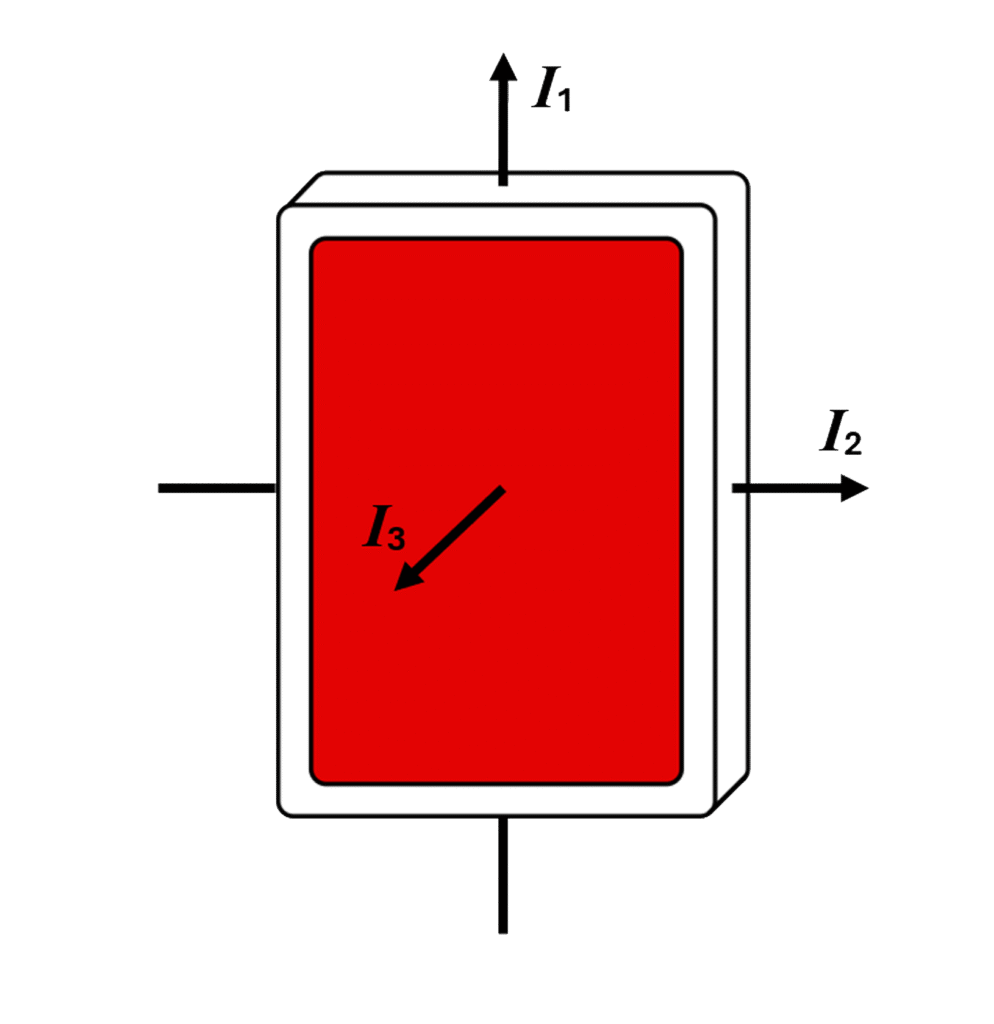
Let us further consider aerial moves that involve rotations – in other words, flourishes with spinning cards or packets. For a rotating packet of cards, there are three axes that it can rotate about, labelled I1, I2 and I3:
For example, the T.G. Murphy Deck Flip rotates the packet along the I1 axis:
…while Flicker Shot rotates the card along the I3 axis:
However, have you ever noticed that there are not many aerial moves that involve spinning cards or packets that rotating along the intermediate I2 axis? Why is that? Is this because cardists, with all their creativity, have somehow overlooked this type of rotation?
Now, before you rush off to quickly invent a flourish involving such a rotation, let me give you a piece of advice: Don’t bother. There’s a very good reason why such rotations aren’t very common in cardistry moves, and it isn’t because of a lack of creativity. It’s because of… PHYSICS!
It turns out that rotations around the I2 axis are actually unstable – hence, aerial moves that have cards spinning along that axis will almost always wobble out of their trajectory, instead of spinning around nicely in a stable fashion. In fact, you can actually deduce that from another classic flourish, Vertigo:
Notice how the packet of cards only spins along two axes – first, a very fast, stable rotation along the I3 axis, followed by a slower but also stable rotation along the I1 axis after the kick. It’s almost like the cards don’t want to spin along that intermediate I2 axis! But why would the I2 axis be an unstable axis?
At this point, you have two options: You can either take my word for it that according to the rigid body stability theorem, rotations of a rigid body around its intermediate principal axis are unstable to small perturbations, or you can scroll on later for the full mathematical derivation. The derivation does require college level physics and mathematics, but I think it’s rather interesting if you can follow along.
But let’s say you’ve chickened out and decided to take my word for it. Let’s do some experiments to hopefully further convince yourself of this statement. (Seriously, do consider scrolling all the way down for the mathematics.)
Firstly, take a deck of cards and do a T.G. Murphy Deck Flip with it, but this time gripping the deck along the short edges (not along the long edges, as you would in a standard dealer’s grip). This will force the deck to attempt to rotate along that I2 axis. Notice how the deck tends to wobble around and not rotate properly? Try it a few times – with a standard Deck Flip, you can flick the deck as hard as you can and the deck will still rotate normally. But try using the same force with the short-edge Deck Flip, and you’ll see the deck wobble out of your hands and perhaps onto the floor!
Let’s do another experiment. Zach Mueller, in his recent video Black Belt, showcased his latest move called Angel Dust:
This is also a move that requires a card to rotate along the unstable I2 axis. Try doing the move for yourself a few times, and you’ll notice that this move is nearly impossible to nail 100% of the time. If I asked you to execute a Flicker Shot or a Deck Flip 20 times in a row without messing up once, I’m sure that won’t be a problem. Just try to nail Angel Dust 20 times in a row – you will not only have problems with catching the card properly, you’ll even have problems making the card rotate properly. And it’s not because of your lack of practice; it’s all down to the PHYSICS. That sort of rotation is inherently unstable, and any small perturbation will cause it to wobble out of shape. So relax – for once, it’s NOT your fault!
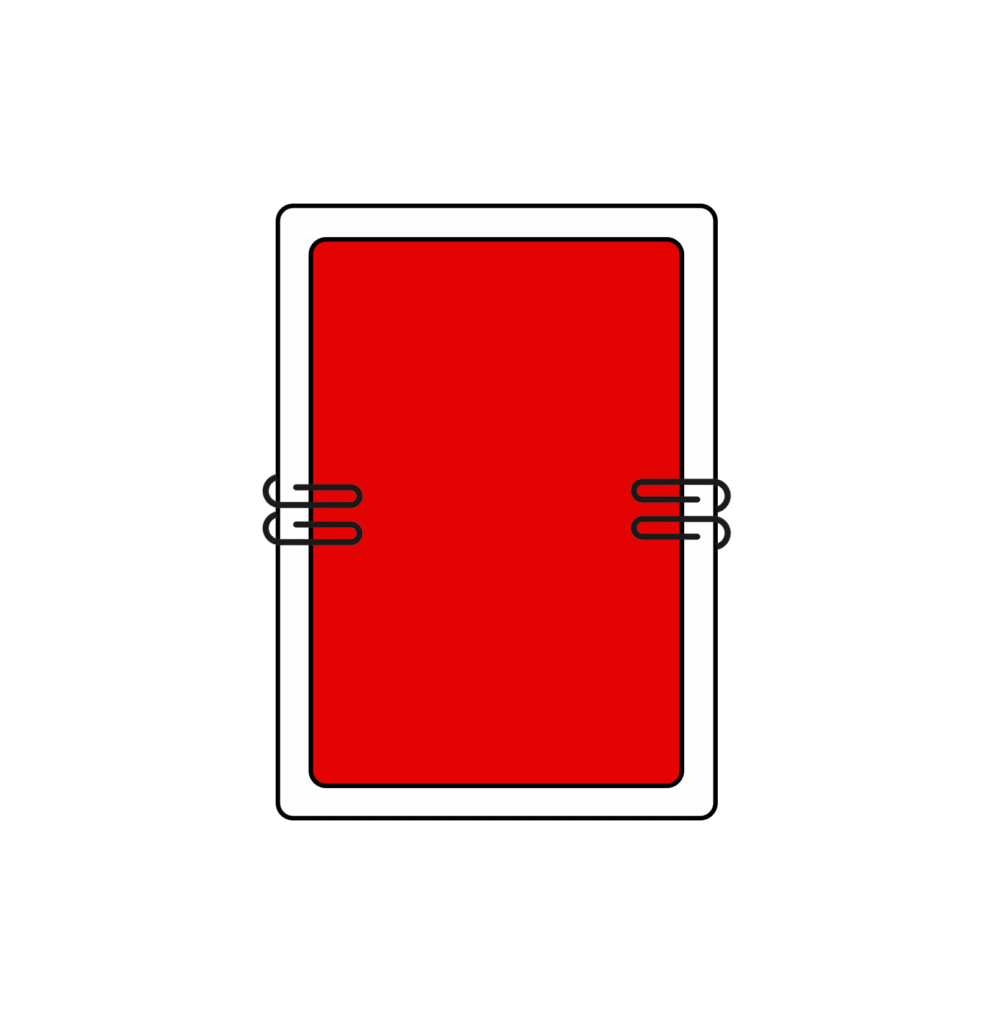
Finally, before we go deep into the mathematics of it, is there any way to overcome this problem with physics? Well, yes and no. Basically, the reason for the instability is due to something called the moment of inertia of the card about its rotation axis. The moment of inertia has to do with the inertia against angular acceleration under an applied torque. The I1 axis has the smallest moment of inertia, while the I3 axis has the largest moment of inertia. As we have stated from the rigid body stability theorem, the intermediate I2 axis has an intermediate moment of inertia and is also the unstable rotation axis. Hence, to overcome the instability, you will need to modify the card’s moments of inertia slightly by attaching a number of paperclips in this manner:
The paperclips modify the card’s moments of inertia, producing stable rotations around the previously unstable axis.
This increases the moment of inertia about the I1 axis so that now, the moment of inertia about the I2 axis is the smallest, making the I1 axis the intermediate axis. This will result in a card that can rotate nicely around the I2 axis (try doing the short edge Deck Flip on such a card), but not rotate properly around the I1axis (a standard Deck Flip on this card will make it wobble out of control). The only problem is that due to the weight of the paperclips, attempting to make it stick to your thumb (as in Angel Dust) is much harder than before.
So what have we learned so far? It seems that with a young art like cardistry, the mantra is “nothing is impossible”. Moves that were deemed way too unreliable, way too impossible or way too crazy a few years ago are now commonplace, due to someone’s dedicated practice and passion. Based on that, it does seem like any move in cardistry is possible with the right amount of practice. However, I think it’s rather interesting to learn that there are some card flourishes that are (and will forever be) inherently more difficult (or perhaps more impossible) than other card flourishes, and I came to this conclusion not after long hours of practicing and failing at a move, but after a few hours of thinking about the physics of spinning cards. Unless you’re a robot, I’d suggest that you watch out for card flourishes that make use of such rotations – these moves are literally impossible to execute 100% of the time.
And we can prove it now… BY SCIENCE!
Still here? Alright, bring on the mathematics. Don’t say I didn’t warn you…
What did you think of the article? Did you dare to click and read through the mathematics? Did you understand it all? Tell us what you think below!